GROVE: https://doi.org/10.1093/gmo/9781561592630.article.06186
Pythagorean tuning and Pythagorean comma
Through the centuries writers on music and music theory have dedicated considerable attention to string divisions, mostly illustrated with the monochord.
Within the approach of Pythagoras the numbers 1, 2, 3 and 4 (called tetraktys) play a key role. These 4 numbers add up to 10.

Applied to the division of a string they result in an octave, pure fifth and pure fourth.
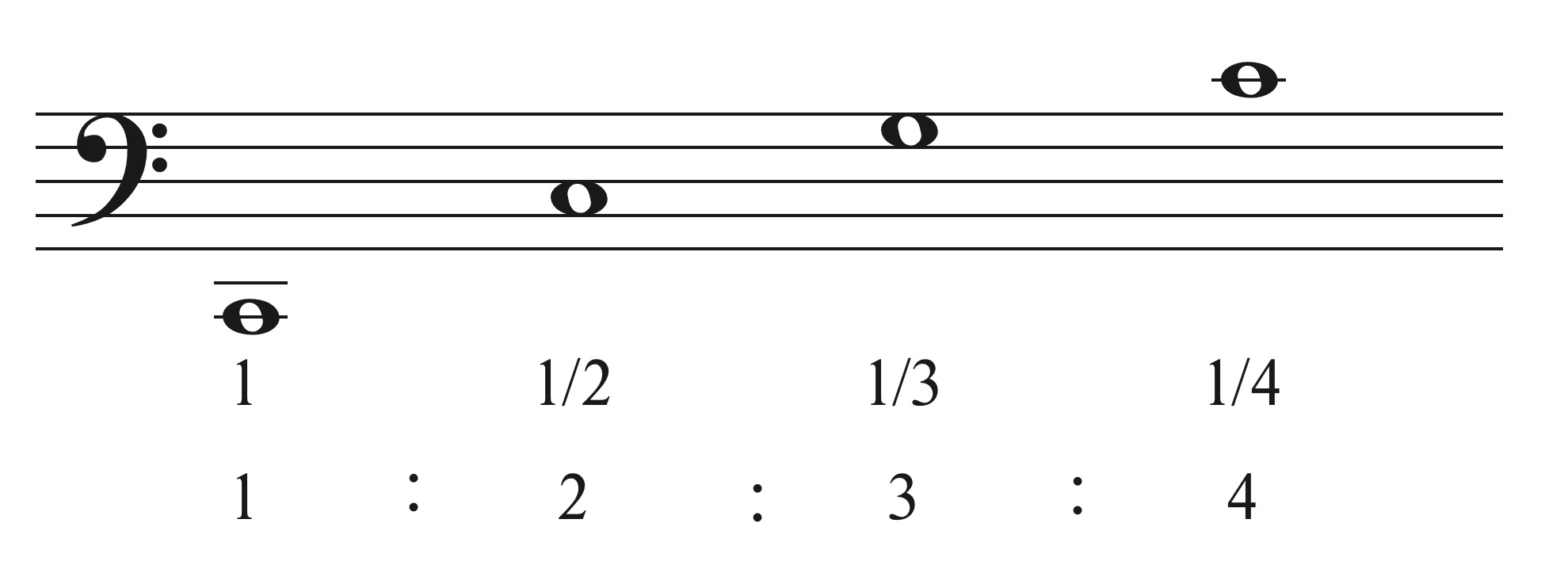
The frequencies of these string lengths relate as 1 : 2 : 3 : 4.
From these proportions it is possible to derive additional tones and, in that way, create tone groups (scales, modes).
So working with pure fifths/fourths and octaves is the point of departure; other intervals result out of combinations of fifths/fourths.
Example of a diatonic scale:
C (basic string length)
c
G
d --> D
A
e --> E
B
c --> F
C-D-E-F-G-A-B-c
When we construct a series of fifths then we arrive at what is called the circle of fifths.
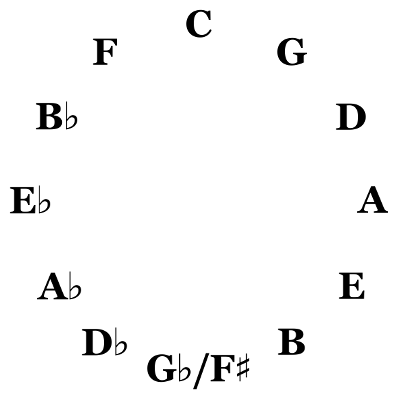
A circle of fifths or fourths results in all 12 pitchclasses.
Now it is given fact of nature that 12 consecutive pure fifths don't form a closed circle.
Pythagorean comma
A sequence of 12 pure fifths does not return on a pure octave of the starting frequency but is considerably higher. In other words: B# ≠ C.
In this context enharmonic "equal" tones are not equal at all. The difference is called a (Pythagorean) comma.
We can prove this in an empirical way by tuning and using our ears, but also by calculating:
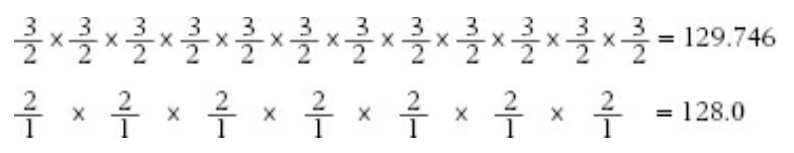
3/2 raised to the power of 12 = 531441/4096 = 129,746338...
2 raised to the power of 7 = 128
| C | G | D | A | E | B | F# | C# | G# | D# | A# | E# | B# |
| Cb | Gb | Db | Ab | Eb | Bb | F | C |
Within our equal temperament the last b# is equal to c, within the Pythagorean tuning there is a clear difference, these tones are (real) enharmonic variants.
The label enharmonic equivalent is thus applicable within equal temperament (modern piano's and the like) but in general musical practice things are not alway as clear cut.
Pythagorean major third
The major third derived from four pure fifths results in a third we experience as (much) too big (stretched).
3/2 raised to the power of 4 = 81/64.
The proportion resulting from string division would be: 5/4 = 80/64
This difference between a Pythagorean and a pure majord third is called a Didymic or syntonic comma.
The equal tempered third is better than the Pythagorean one, but not as good as the pure one.
String players playing thirds and sixths with double stops, always aim at removing beats from the sounding interval; they aim to play with just intonation.



